|
4. Congruences
Let A be an algebraic category.
Let X be an object. Denote by X2 the product
X  X. If U is a subset of X2 we denote by p,
q: U --> X the maps induced by the projections X2
--> X.
X. If U is a subset of X2 we denote by p,
q: U --> X the maps induced by the projections X2
--> X.
Remark 4.1. Recall that an equavlence
relation on a set X is a subset U of X2
satisfying the following conditions: (1) (a, a)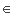 U for any a in X.
U for any a in X.
(2) If (a, b)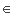 U
then (b, a) U
then (b, a)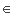 U. U.
(3) If (a, b), (b, c)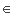 U,
then (a, c) U,
then (a, c)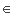 U. U.
(a) If U is an equavelence relation on X, we denote by
X/U
the quotient set of X under U, and q: X --> X/U
the canonical surjective map. Then U = X  X/U
X. X/U
X.
(b) A subset U of X2 is an equivalence relation
iff U = X  T
X for a map t: X --> T (we may assume t is surjective). T
X for a map t: X --> T (we may assume t is surjective).
(c) Any intersection of equivalence relations is an equivalence.
Definition 4.2. (a) An equavelence relation
on X is called a congruence
if it is a closed subset of X2.
(b) A subset U of X2 is called an effective
congruence on X if there is a (surjective) morphism t:
X --> T such that U = X  T
X. T
X.
Proposition 4.3. An effective congruence
is a congruence.
Proof. If t: X --> T is a morphism then X  T
X is a closed subset of X2 by (3.6), which is also
an equavelence relation on X by (4.1.c). T
X is a closed subset of X2 by (3.6), which is also
an equavelence relation on X by (4.1.c).
Example 4.3.1. If X is a set
in Set, a subset U of X2 is a congruence
iff it is an equivalence relation on X .
Proposition 4.4. An equivalence relation
u,
v: U --> X is an effective congruence on X iff there
is a structure on the quotient X/U such that q: X -->
X/U is a morphism.
Proof. Since U = X  X/U
X by (4.1.a), if q is a morphism then U is an effective
congruence. Conversely, assume U = X X/U
X by (4.1.a), if q is a morphism then U is an effective
congruence. Conversely, assume U = X  T
X for a morphism t: X --> T, then X/U = t(X)
by (4.1) and X --> t(X) is a morphism by (2.5). T
X for a morphism t: X --> T, then X/U = t(X)
by (4.1) and X --> t(X) is a morphism by (2.5).
Proposition 4.5. Any intersection of congruences
is a congruence.
Proof. This follows from the fact that the classes of equavelnce
relations and closed subsets are closed under intersections.
Proposition 4.6. Any intersection of effective
congruences is an effective congruence.
Proof. For any equivalence relation u, v: U -->X
let q: X --> X/U be the quotient map. Let
g: X/U
--> G be the generic extensiion of q. Then
gq: X -->
G is a morphism. Let C(U) = X  G
X. Then C(U) is an effective congruence. We show that C(U)
is the smallest effective congruence containing
U. Suppose V
is another effective congruence on X containing U. The quotient
map p: X --> X/V factors through q: X --> X/U
by a map t: X/U --> X/V. Then by the property of the generic
extention g there is a unique morphism s: G --> X/V
such that t = sg. Thus p = tq =sgq, which shows that V
contains C(U). G
X. Then C(U) is an effective congruence. We show that C(U)
is the smallest effective congruence containing
U. Suppose V
is another effective congruence on X containing U. The quotient
map p: X --> X/V factors through q: X --> X/U
by a map t: X/U --> X/V. Then by the property of the generic
extention g there is a unique morphism s: G --> X/V
such that t = sg. Thus p = tq =sgq, which shows that V
contains C(U).
Next consider the intersection U of a set {Ui}
of effective congruences on X. We have C(U)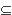 C(Ui)
= Ui for any Ui. It follows that C(U)
is contained in the intersection of {Ui}, which is U.
This shows that U is an effective congruence. C(Ui)
= Ui for any Ui. It follows that C(U)
is contained in the intersection of {Ui}, which is U.
This shows that U is an effective congruence.
Definition 4.7. A variety
is an algebraic category such that any congruence is effective.
[References][Notations][Home]
|