Let C be a category and 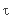 a covariant functor from C to a category of topological spaces. We are interested in the geometry of C imposed by 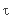. In practice the functor 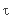 always comes from the underlying topology of the objects, therefore should be regarded as an invariant of C. 

We introduce the concept of a metric site, which is a pair (C, 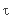) satisfying certain categorical-geometric properties. A metric site has enough local isomorphisms (called effective morphisms), so that the open effective covers generate a Grothendieck topology (in the sense of [SGA4]). Virtually all the major categories arising in modern geometry are metric sites, and many results obtained by Grothendieck in [EGAI] for schemes can be reformulated and proved for the objects of any metric site. Therefore we believe it is worth to develop a general theory of metric sites, which will provide a categorical foundation for modern geometry (see [Luo 1998]). 

In a metric site we are able to glue objects directly in categorical terms (instead of "glueing charts" in differential geometry, or "glueing sheaves" in algebraic geometry). We study the phenomenon associated with the glueing procedures in º2, introducing the concepts of strict and complete metric sites. As in the theory of metric spaces, afundamental fact in this direction is the following theorem concerning the completion of a metric site (see º3): 
 
Theorem. Any strict metric site Chas a completion, which is uniquely determined byC up to equivalence. The collection of so called Dedekind cuts forms a completion of C, and C is complete if and only if any Dedekind cut of C is representable. If fibre products exist in C, then fibre products exist in any completion of C.

We mention another approach to the theory of metric sites. Recall that a frame is a complete lattice with infinite distributive law, and a morphism of frames is a map of lattices preserving finite meets and arbitrary joints (see [Johnstone 1982]). We define a framed site to be a category together with a function which assigns to each object a frame of sieves in a continuous way. For instance, every elementary topos is naturally a framed site (assigning to each object t he frame of its subobjects). Using the language of framed sites we can give an intrinsic definition for a sober metric site (see [Luo 1995b]).