1.4. Coflat Maps 

Definition 1.4.1. (a) A map f: Y --> X is called precoflat if the pullback of any epi to X along f is epic. 
(b) A map f: Y --> X is called coflat if the pullback of f along any map to X is precoflat. 

Equivalently, a map f: Y --> X is coflat if the pullback functor A/X --> A/Y along f preserves epis. 

Proposition 1.4.2.  (a) Coflat maps are stable, i.e. the pullback of a coflat map is coflat. 
(b) Composite of coflat maps are coflat. 
(c) Finite products of coflat maps are coflat. 
(d) A finite sum of maps is coflat iff each factor is coflat. 

Proof. (a) and (b) are immediate. 
(c) Let f1: Y1 --> X1 and f2: Y2 --> X2 be two coflat maps. Consider the following pullback: 

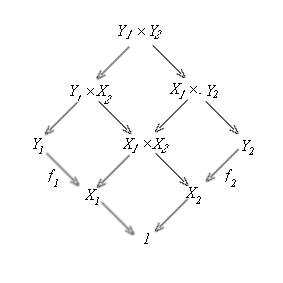
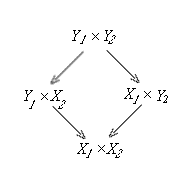
Since f1: Y1 --> X1 and f2: Y2 --> X2 are coflat and the pullbacks of coflat maps are coflat, Y1  X2 --> X1  X2 and X1  Y2 --> X1  X2 are coflat. It follows that the cartisian diagram 
consists of coflat maps. Thus (f1  f2): Y1  Y2 --> X1  X2 is coflat by (b). 
(d) Consider two maps u1: X1 --> T1 and u2: X2 --> T2 . If u1 + u2 is coflat, then u1 and u2 are coflat by (a) because they are pullbacks of u1 + u2 by (1.3.4.b). Conversely assume u1 and u2 are coflat. Any map from g to T1 + T2 has the form g = v1 + v2: Y1 + Y2 --> T1 + T2 for two maps v1: Y1 --> T1 and v2: Y2 --> T2. Then by (1.3.4.a) the pullback s of g along u1 + u2 is the sum of X1 T1 Y1 --> X1 and X2 T2 Y2 --> X2 . If g is epic then v1 and v2 are epic by (1.3.7), thus X1 T1 Y1 --> X1 and X2 T2 Y2 --> X2 are epic because u1 and u2 are coflat. It follows that s is epic by (1.3.7). This shows that u1 + u2 is precoflat. Next the pullback t of u1 + u2 along g is the sum of the coflat map X1 T1 Y1 --> Y1 and the coflat map X2 T2 Y2 --> Y2. Thus t is also precoflat. It follows that u1 + u2 is coflat. 

Proposition 1.4.3. (a) Suppose f: Y --> X is a mono and g: Z --> Y is a map. Then g is coflat if fg is coflat. 
(b) For any object X, the codiagonal map X: X + X --> X is coflat. 
(c) Suppose {fi: Yi --> X} is a finite family of coflat maps. Then f =  (fi): Y =  Yi --> X is coflat. 

Proof. (a) If fg is coflat then g is coflat as it is the pullback of fg along f. 
(b) The pullback of X: X + X --> X along a map Z --> X is the map Z: Z + Z --> Z . Therefore in order to show that X  is coflat it suffices to prove that X is precoflat. Assume f: Y --> X is an epi. Then the pullback of f along X is f + f: Y + Y --> X + X, which is an epi by (1.3.7). 
(c) For any pair of coflat maps f: Y --> X and g: Z --> X the induced map (f, g): Y + Z --> X is the composite of the coflat maps f + g: Y + Z --> X + X and X: X + X --> X by (b) and (1.4.2.d). Thus (f, g) is coflat. This result extends immediately to a map of the form f = (fi): Y =  Yi --> X. 

Recall that a map in a category is a bimorphism if it is both epic and monic. 

Proposition 1.4.4. (a) Coflat monos are stable. 
{b} Composites of coflat monos (bimorphisms) are coflat monos (bimorphisms). 
(c) Finite intersections of coflat monos (bimorphisms) are coflat mono (bimorphisms). 
(d) A finite sum of monos (bimorphisms) is a coflat mono (bimorphisms) iff each factor is a coflat mono (bimorphisms). 
(e) Suppose f: Y --> X is a coflat bimorphisms. If g: Z --> Y is a map such that fg is an epi, then g is an epi. 
(f) Suppose f: Y --> X is a coflat mono (bimorphisms) and g: Z --> Y is any map. Then g is a coflat mono (bimorphisms) iff fg is a coflat mono (bimorphisms). 

Proof. (a) - (d) follows from (1.4.2), (1.3.7) and (1.3.8). 
(e) Since f is a mono and fg factors through f, (g, 1Z) is the pullback of (f, fg). If fg is an epi then g is an epi as f is coflat by assumption. 
(f) follows from (e) and (1.4.3.a). 

Proposition 1.4.5. Injections of a sum are coflat monos. 

Proof. The injection X --> X + Y is the sum of the coflat mono 1X: X --> X and the coflat mono 0 --> Y . Thus by (1.4.4.d) it is coflat. 
 
 

 [Next Section][Content][References][Notations][Home]