|
4.1. Locally Finitely Copresentable Categories
Recall that a set 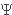 of
objects in a category A is called a
cogenerating set provided that for a pair of maps (r1,
r2): X --> T such that r1 of
objects in a category A is called a
cogenerating set provided that for a pair of maps (r1,
r2): X --> T such that r1 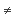 r2 there exists an object R
r2 there exists an object R 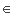 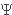 and a map g: T --> R such that gr1
and a map g: T --> R such that gr1 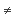 gr2. If
gr2. If 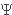 is a small set we say that
is a small set we say that 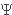 is a small cogenerating set. If
is a small cogenerating set. If 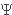 consists of a single object T then T is called a cogenerator
for A. A cogenerating set
consists of a single object T then T is called a cogenerator
for A. A cogenerating set 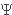 is called strong
provided that for each object X and each proper quotient of
X there exists a map X --> R
with R
is called strong
provided that for each object X and each proper quotient of
X there exists a map X --> R
with R 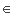 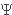 which does not factorize through that quotient.
which does not factorize through that quotient.
Suppose A is complete. Then a small set 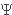 of objects is a cogenerating set iff every object is a subobject of a product
of objects in
of objects is a cogenerating set iff every object is a subobject of a product
of objects in 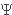 ; ; 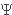 is a strong cogenerating set iff every
object is a strong subobject of a product of objects in
is a strong cogenerating set iff every
object is a strong subobject of a product of objects in 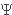 .
We say a set .
We say a set 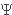 of objects
is a regular
cogenerating set
if every object is a regular subobject of a product of objects in of objects
is a regular
cogenerating set
if every object is a regular subobject of a product of objects in 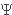 . .
An object X of a category A is finitely
copresentable provided that the functor hom(~, X):
Aop --> Set preserves directed colimits
(or filtered colimits).
Definition 4.1.1. A category A
is called locally
finitely copresentable if it is cocomplete and has a small set
of finitely copresentable objects such that every object is an inverse
limit of objects in the set.
The dual notion is a locally finitely presentable
category.
We summarize the properties of a locally finitely copresentable category
A which will be needed below (see [Gabriel
and Ulmer 1971], [Johnstone 1982],
[Adamek and Rosicky 1994], or [Borceux
1994, Vol II]):
Remark 4.1.2. (a) A is complete
and cocomplete.
(b) Each object X has a small set of subobjects. Since the category
is complete, this implies that any intersection of subobjects exist. Consequently,
any intersection of strong subobjects exist, i.e. A is perfect.
(c) The full subcategory Fin(A)
of finitely copresentable objects is closed under finite limits and is
essentially small (i.e. with a small skeleton).
(d) Any map has an epi-strong-mono
factorization (see (1.2.2.c)).
(e) A complete category is locally finitely copresentable iff every
object is an inverse limit of finitely copresentable objects and there
exists, up to isomorphism, only a small set of finitely copresentable object
(i.e. the full subcategory Fin(A) of
finitely copresentable objects is essentially small).
(f) A complete category is locally finitely copresentable iff it has
a small strong cogenerating set formed by finitely copresentable objects.
(e) If C is an essentially small category
with finite limits we denote by Cart(C. Set)
the category of finite-limit-preserving functors from C
to Set. Then the opposite Cart(C,
Set)op of Cart(C,
Set) is locally finitely copresentable and
C is equivalent to the subcategory of finitely
copresentable objects of Cart(C, Set)op.
Any locally finitely copresentable category A is
equivalent to Cart(Fin(A). Set)op.
Let A be a locally finitely copresentable category. A regular
subobject (or regular mono) of an object is called finitely
cogenerated if it is the equalizer of a pair of maps with a
finitely copresentable object as codomain.
Proposition 4.1.3. (a) Any regular subobject
is an intersection of finitely cogenerated regular subobjects.
(b) Any pullback of a finitely cogenerated regular subobject is finitely
cogenerated.
(c) Any finite intersection of finitely cogenerated regular subobjects
is finitely cogenerated.
Proof. (a) The collection of finitely copresentable objects is
a set of cogenerators for A. Thus the assertion follows from (1.7.6).
(b) follows from the definition.
(c) Suppose u is a finite intersection of finitely cogenerated
regular subobjects {ui: Ui --> X},
such that each ui is an equalizer of a pair of maps (ri,
si): X --> Vi with finitely copresentable
Vi. Let V be the products of Vi.
Then V is also finitely copresentable by (4.1.2.c).
Let r: X --> V be the map induced by the maps {ri},
and let s: X --> V be the map induced by the maps {si}.
Then u is the equalizer of (r, s): X --> V with a
finitely copresentable codomain. Thus u is finitely cogenerated.
Proposition 4.1.4. The following conditions
are equivalent for a regular subobject V of an object X:
(a) V is finitely cogenerated.
(b) If the intersection of a collection {Vi} of regular
subobjects is contained in V, then a finite intersection of objects
in {Vi} is contained in V.
Proof. First assume v: V --> X is the equalizer
of a pair of maps (r, s): X --> C with a finitely copresentable
codomain C. Suppose the intersection w: W --> X of
a collection {wi: Wi --> X} of strong
subobjects is contained in v. Let {wj: Wj
--> X} be the collection of finite intersections of wi.
Then w is the limit of the cofiltered systems {wj}.
Since rv = sv, we have rw = sw. Since C is finitely
copresentable, there is an object wj: Wj
--> X such that rwj = swj. Since v
is the equalizer of (r, s), wj is contained in
v. Since wj is a finite intersection of objects
in {Wi}, this prove that (a) implies (b).
Conversely, assume v: V --> X satisfies the condition
(b). Since v is an intersection of finitely cogenerated regular
subobjects by (4.1.3.a), it is a finite intersection
of such subobjects. Thus v is finitely cogenerated by (4.1.3.c).
Proposition 4.1.5. Any composite of
finitely cogenerated monos is finitely cogenerated.
Proof. Suppose U is a finitely cogenerated regular subobject
of an object X and V a finitely cogenerated regular subobject
of U. Consider a collection {Vi} of regular subobjects
of X whose intersection is contained in V. Since the intersection
of {Vi  U}
is in V and V is finitely cogenerated in U, we can
find a finite set {V1s U}
is in V and V is finitely cogenerated in U, we can
find a finite set {V1s  U} whose intersection is in V. Since U is
finitely cogenerated and the intersection of {Vi} is
in U, we can find a finite set {V2s} whose intersection
is in U. Then the intersection of the finite set {V1s,
V2s} is contained in the intersection of {V1s
U} whose intersection is in V. Since U is
finitely cogenerated and the intersection of {Vi} is
in U, we can find a finite set {V2s} whose intersection
is in U. Then the intersection of the finite set {V1s,
V2s} is contained in the intersection of {V1s  U}, thus is in V. This shows that V is finitely cogenerated
in X by (4.1.4).
U}, thus is in V. This shows that V is finitely cogenerated
in X by (4.1.4).
Recall that a non-empty partially ordered set (i.e. a poset) is called
directed if each pair of elements has an upper bound. An element
s of a poset (S, 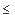 )
is called finite (or compact) provided that for each directed set T )
is called finite (or compact) provided that for each directed set T 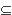 S with s
S with s 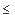 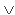 T there exists t
T there exists t 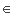 T such that s
T such that s 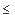 t. An algebraic lattice is a poset (S,
t. An algebraic lattice is a poset (S, 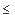 )
which is cocomplete and every element is a directed join of finite elements. )
which is cocomplete and every element is a directed join of finite elements.
Proposition 4.1.6. The dual of the lattice
of regular subobjects of an object is an algebraic lattice.
Proof. It follows from (4.1.4) that a finitely
cogenerated subobject is a compact element in the dual of the lattice of
regular subobjects of an object. The assertion then follows from (4.1.3.a).
Suppose 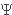 is a small strong cogenerating set formed by finitely copresentable
objects. A regular subobject (or regular mono) of an object is called
is a small strong cogenerating set formed by finitely copresentable
objects. A regular subobject (or regular mono) of an object is called 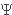 -principal
if it is the equalizer of a pair of maps with a finitely copresentable
object in -principal
if it is the equalizer of a pair of maps with a finitely copresentable
object in 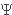 as codomain. The proof of the following proposition is similar to
that of (4.1.3):
as codomain. The proof of the following proposition is similar to
that of (4.1.3):
Proposition 4.1.7. (a) Each 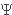 -principal
regular subobject is finitely cogenerated. -principal
regular subobject is finitely cogenerated.
(b) Any regular subobject is an intersection of 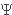 -principal
regular subobjects. -principal
regular subobjects.
(c) Any pullback of a 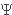 -principal
regular subobject is -principal
regular subobject is 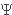 -principal. -principal.
[Next Section][Content][References][Notations][Home]
|