|
4. Prime Ideals
Let C be any category.
Definition 4.1. Suppose p is a
proper radical ideal of an object X.
(a) p is called irreducible
if for any two ideals a and b of X, a  b
b 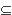 p
implies that a or b is in p. p
implies that a or b is in p.
(b) p is called prime if
for any arrow t: Y --> X, f-1(p)
is irreducible.
(c) An object X is called integral
if 0X is a prime ideal.
Remark 4.2. (a) If f: Y -->
X is an arrow and p is a prime ideal then f-1(p)
is a prime ideal.
(b) If X is integral and f: Y --> X is a monomorphism,
then Y is also integral (i.e. any subobject of a integral object
is integral).
Denote by Spec(X) the set of prime ideals for an object
X. Any arrow f: Y --> X induces a map Spec(f):
Spec(X) --> Spec(Y) sending each prime ideal p
of X to the prime ideal f-1(p) of Y.
If a is any ideal of X we define the subset V(a) 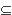 Spec(X) to be the set of all prime ideals which contain a.
Spec(X) to be the set of all prime ideals which contain a.
Proposition 4.3. (a) If a and b
are two ideals, then V(a  b) = V(a)
b) = V(a) 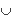 V(b).
V(b).
(b)} If {ai} is any set of ideals of X,
then V(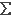 ai)
= ai)
=  V(ai). V(ai).
(c) V(1X) = 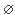 and V(0X) = Spec(X).
and V(0X) = Spec(X).
Proof. (a) If p Î
V(a  b)
we have p b)
we have p 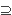 a a  b. Then a or b is in p as p is prime.
Thus V(a
b. Then a or b is in p as p is prime.
Thus V(a  b)
b) 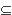 V(a) V(a) 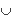 V(b). The other direction is trivial.
V(b). The other direction is trivial.
(b) and (c) are obvious.
It follows from (4.3) that the subsets of the form
V(a) are the closed subsets of a topology on Spec(X),
which turns Spec(X) into a topological space.
Proposition 4.4. Suppose f:
Y --> X is an arrow. Then Spec(f): Spec(X)
--> Spec(Y) is a continuous map.
Proof. If a is any ideal of Y, then we have f-1(V(a))
= V(f(a)). Thus Spec(f) is continuous.
It follows from (4.4) that Spec is a natural contravariant functor
from C to Top.
Definition 4.5. An ideal is called spatial
if it is an intersection of prime ideals.
Remark 4.6. (a) Any prime ideal is spatial
and any spatial ideal is radical by (3.5.a).
(b) Any intersection of spatial ideals is spatial (thus 1X
is spatial).
(c) The inverse image of a proper spatial ideal along any arrow is
a proper spatial ideal.
Proposition 4.7. Any irreducible spatial
ideal is prime.
Proof. Suppose p is an irreducible spatial ideal of an
object X and f: Y --> X is an arrow. We prove that
f-1(p) is irreducible. First f-1(p)
is proper and radical since it is an intersection of proper radical ideals.
Suppose a and b are two ideals of Y such that a  b
b 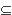 f-1(p).
Suppose q is a prime ideal of X containing p. Then
f-1(q) is a prime ideal containing f-1(p).
Thus a or b is in f-1(q). It follows
that f*(a) or f*(b) is
in q. Thus q contains f*(a) f-1(p).
Suppose q is a prime ideal of X containing p. Then
f-1(q) is a prime ideal containing f-1(p).
Thus a or b is in f-1(q). It follows
that f*(a) or f*(b) is
in q. Thus q contains f*(a)  f*(b). Since p is an intersection of such
q, we see that p contains f*(a)
f*(b). Since p is an intersection of such
q, we see that p contains f*(a)  f*(b). Since p is irreducible, f*(a)
or f*(b) must be contained in p. Hence
a or b is in f-1(p). This proves
that f-1(p) is irreducible. Thus p is prime.
f*(b). Since p is irreducible, f*(a)
or f*(b) must be contained in p. Hence
a or b is in f-1(p). This proves
that f-1(p) is irreducible. Thus p is prime.
Proposition 4.8. Spec(X)
is a sober space.
Proof. Suppose W is an irreducible closed subset of Spec(X).
Let p be the intersection of all the prime ideals in V. Then
W = V(p). Suppose a and b are two ideals of
X and p 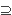 a a  b. Then W = V(p)
b. Then W = V(p) 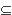 V(a Ç b)
= V(a)
V(a Ç b)
= V(a) 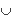 V(b).
Since W is irreducible, we must have W V(b).
Since W is irreducible, we must have W 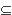 V(a) or W
V(a) or W 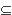 V(b).
But W V(b).
But W 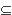 V(a) means
that any prime ideal in W contains a. Since p is the
intersection of all the prime ideals in W, we have p V(a) means
that any prime ideal in W contains a. Since p is the
intersection of all the prime ideals in W, we have p 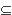 a. Similarly W
a. Similarly W 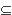 V(b) implies that p
V(b) implies that p 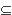 b. Thus we have p
b. Thus we have p 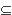 a or p
a or p 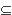 b. It follows that p is irreducible. Since p is
spatial, it is prime by (4.7). Clearly p is the
generic point of W. This proves that Spec(X) is sober.
b. It follows that p is irreducible. Since p is
spatial, it is prime by (4.7). Clearly p is the
generic point of W. This proves that Spec(X) is sober.
Definition 4.9. The intersection s(a)
of all the prime ideals containing a set a of 2-elements
of X is called the spatial radical of
a.
Proposition 4.10. (a) Suppose {ai}
is a set of ideals of X. Then for any ideal a of X
we have
s(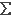 i
a i
a  ai)
= s(a) ai)
= s(a)  s( s(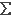 i
ai).
Suppose f: Y ® X is
an arrow and a, b are two ideals of Y. Then
s(f(a i
ai).
Suppose f: Y ® X is
an arrow and a, b are two ideals of Y. Then
s(f(a  b)) = s(f(a))
b)) = s(f(a))  s(f(b)).
Proof. We only need to verify that s(
s(f(b)).
Proof. We only need to verify that s(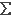 i
a i
a  ai) ai) 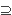 s(a)
s(a)  s(
s(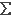 i ai).
Suppose p is a prime ideal containing each a i ai).
Suppose p is a prime ideal containing each a  ai. Then p contains a or each
ai. It follows that p contains s(a)
or s(
ai. Then p contains a or each
ai. It follows that p contains s(a)
or s(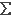 i ai).
Hence p contains s(a) i ai).
Hence p contains s(a)  s(
s(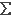 i ai).
This proves the assertion. i ai).
This proves the assertion.
(b) We only need to verify that s(f(a  b))
b)) 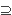 s(f(a)) s(f(a))  s(f(b)). Suppose p is a prime ideal containing
f(a
s(f(b)). Suppose p is a prime ideal containing
f(a  b).
Then f-1(p) contains a b).
Then f-1(p) contains a  b. Since f- 1(p) is prime, it contains
a or b. Then p contains f(a) or (f(b).
Thus it contains s(f(a)) or s(f(b)).
It follows that p contains s(f(a))
b. Since f- 1(p) is prime, it contains
a or b. Then p contains f(a) or (f(b).
Thus it contains s(f(a)) or s(f(b)).
It follows that p contains s(f(a))  s(f(b)).
s(f(b)).
Corollary 4.11. (a) For each object X
the set Is(X) of spatial ideals of X
is a spatial frame.
(b) For any arrow f: Y --> X the map Is(Y)
--> Is(X) sending each spatial ideal
a of Y to the spatial ideal s(f(a))
of X is a map of frames.
(c) Is(X) is isomorphic to the frame
of open subsets of Spec(X).
Proof. (a) and (b) follow from (4.10).
(c) follows from the fact that if a and b are two ideals
of an object X, then V(a) = V(b) if
and only if s(a) = s(b) . Note that
(a) and (b) also follow from (c).
Definition 4.12. (b) A category is spectral
if any non-terminal object has a prime ideal.
(b) A category is integral if any
non-terminal object is integral (note that any integral category is spectral).
Proposition 4.13. Any spectral
category is radical.
Proof. Suppose f: X --> T is an arrow and T
is non-terminal. Then f*(1X) 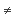 0T because T has
a prime ideal p and f- 1(p) is prime, which
is proper. Thus the category is unitary by (2.9.b).
Since each non-terminal object has a prime ideal which is radical and proper,
the category is radical.
0T because T has
a prime ideal p and f- 1(p) is prime, which
is proper. Thus the category is unitary by (2.9.b).
Since each non-terminal object has a prime ideal which is radical and proper,
the category is radical.
Proposition 4.14. Suppose C is
a spectral category.
(a) Any proper ideal is contained in a prime ideal.
(b) Any maximal ideal is prime.
Proof. (a) Any proper ideal is contained in a proper 2-kernel
ker(f) of an arrow f: X --> Z, and ker(f)
is contained in the inverse image of any prime ideal of Z.
(b) follows from (a).
Proposition 4.15. An ideal of an object
in a spectral category is radical if and only if it is spatial.
Proof. Suppose a is a proper radical ideal of X.
For any 2-element r of X not in a let t:
X --> Z be an arrow such that t(r) is invertible and
t(a) is not. Let p be a prime ideal of Z containing
t(a). Then f- 1(p) is a prime ideal
containing a but not r. This shows that a is an intersection
of prime ideals. The other direction follows from (4.6.a).
Corollary 4.16. (a) In a spectral category
we have r(a) = s(a) for any ideal
a.
(b) A proper radical ideal in a spectral category is prime if and only
if it is irreducible.
Proof. (a) follows from (4.15).
(b) is a consequence of (4.7) and (4.15).
[Next Section][Content][References][Notations][Home]
|