In this section we recall some basic properties of strong monos in a category with pullbacks. Please note that the notion of a strong mono is also defined for a general category (cf. Adamek, Herrlich and Strecker 1990] or [Borceux 1994 Vol I]). However, for our purpose the following simplified approach is sufficient. 

Definition 1.1.1. (a) A strong mono is a map such that any of its pullbacks is not non-isomorphic epic. 
(b) A regular mono is a map which can be written as the equalizer of some pair of maps. 

Proposition 1.1.2. (a) Any strong mono is a mono. 
(b) An epic strong mono is an isomorphism. 
(c) Any pullback of a strong mono is a strong mono. 
(d) Any composite of strong monos is a strong mono. 
(e) Any intersection of strong monos is a strong mono. 

Proof. (a) If f: Y ® X is not a mono then its pullback along itself is a non-isomorphic epi (a retraction). Thus f is not a strong mono. 
(b) and (c) by definition. 
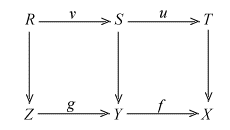
(d) Suppose f: Y ® X and g: Z ® Y are two strong monos. Suppose an epi w: R ® T is the pullback of f_°g along a map t: T ® X. We have to prove that w is an isomorphism. Let u: S ® T be the pullback of f along t. Then w factors through u in a map v: R ® S, and u is an epi because w is so. Then u is an isomorphism as f is a strong mono. From w = u_°v we conclude that v is an epi. But g is a strong mono and v is a pullback of g. So v is also an isomorphism. This shows that w = u_°v is an isomorphism. 

Proof.  (a) If u: U ® X is the equalizer of a pair of maps (s, t): X ® Z and f: Y ® X is any map then the pullback of u along f is the equalizer of (s_°f, t_°f). 
(b) A map f: Y ® X is not epic iff there is a pair of different maps (s, t): X ® Z such that s_°f = t_°f , in which case f factors through the equalizer of (s, t), which is a non-isomorphic regular mono. 
(c) A regular mono is not non-isomorphic epic by (b) and any pullback of a regular mono is a regular mono by (a). 
(d) follows from (b) as any non-isomorphic strong mono is not epic. 
(e) follows from (b) - (d). n 

If a map f: Y ® X in a category is the composite m_°e of an epi e: Y ® T followed by a strong (resp. regular) mono m: T ® X  then the pair (e, m) is called an epi-strong-mono (resp. epi-reg-mono) factorization of f; the codomain T of e is called the strong (resp. regular)  image of f. We say a category has epi-strong-mono (resp. epi-regular-mono) factorizations if any map has such a factorization. 

Proposition 1.1.4.  (a) Suppose f: Y ® X is a map which is the composite of a map e: Y ® U and a strong mono m: U ® X. Then e is epic iff m is the smallest strong mono to X which f factors through. 
{b} Assume any composite of regular monos is regular. Suppose f: Y ® X is a map which is the composite of a map e: Y ® U and a regular mono m: U ® X. Then e is epic iff m is the smallest regular mono to X which f factors through. 
{c} An epi-strong-mono (resp. epi-reg-mono) factorization of a map is unique up to isomorphism. 

Proof. (a) follows from (1.1.2.d) and (1.1.3.e); (b) can be proved similarly using (1.1.3.b); (c) follows form (a) and (b). n 
 
Proposition 1.1.5. Consider a category A with pullbacks. 
(a) A has epi-strong-mono factorizations if any intersection of strong monos exists. 
(b) A has epi-regular-mono factorizations if the class of regular monos is closed under composition and intersection. 
(c) A has epi-regular-mono factorizations if any composite of regular monos is a regular mono and any map has a cokernel pair. 
(d) If A has epi-regular-mono factorizations then any strong mono is regular. 
 
Proof.  (a) Any map f: Y ® X can be factored as a map e: Y ® U followed by a mono m: U ® X, where m is the intersection of all the strong monos in which f can be factored through. Then m is a strong mono by (1.1.2.e) and e is an epi by (1.1.4.a). 
(b) Similar to (a). 
(c) Any map f: Y ® X can be factored as a map e: Y ® U followed by a regular mono m: U ® X, which is the equalizer of the cokernel pair of f. Then m is the smallest regular mono such that f factors through. Thus e is epic by (1.1.4.b). 
(d) follows from (1.1.4.c). n