Suppose A is a category with a strict initial object 0. Consider a functor G from A to the category of locales.
Definition 2.5.1. A mono u:
U ® X in A
and its image G(u): G(U)
® G(X)
is called open
effective if the following conditions are satisfied:
(a) G(u) is an open embedding of
locales.
(b) If t: T ® X
is a map in A such that G(t)
factors through G(u) then t factors
through u (uniquely).
If u is open effective then u or U is called an open effective subobject of X, and G(u) or G(U) is an open effective sublocale of G(X).
Definition 2.5.2. A framed
topology on A is a functor G
from A to the category of locales, satisfying
the following conditions:
(a) An object X is initial iff G(X)
is initial.
(b) Any open sublocale of G(X) is
a join of open effective sublocales of G(X).
A framed topology G is spatial if for any object X the locale G(X) is spatial.
Example 2.5.2.1. (a) The identity
functor on the category of locales is a framed topology.
(b) The functor on the category of topological spaces sending each
topological space to the locale of its open sets is a spatial framed topology.
Suppose G is a framed topology on A. If {Ui} is a set of open effective subobjects of X such that G(X) is the join of {G(Ui)}, then we say that {Ui} (resp. {G(Ui)}) is an open effective cover on X (resp. G(X)).
Proposition 2.5.3. Suppose u:
U ® X is an open effective mono
and t: T ® X is a map.
(a) t is disjoint with u iff G(t)
is disjoint with G(u) (i.e. G(t)-1(G(U)
= 0).
(b) If u is a normal mono then t is dominated by u
iff G(t) factors through G(u).
Proof. (a) If s: S ®
X is a map factors through both u and t then G(s):
G(S) ®
G(X) factors through G(t)-1(G(U)),
so s must be initial if G(t)-1(G(U))
= 0 by (2.5.2.a). Conversely if the open sublocale
G(t)-1(G(U)
¹ 0 then it is a join of non-initial
open effective sublocales {vi: Vi ®
T} by (2.5.2.b), and each t°vi
factors through both u and t. Thus t is not disjoint
with u.
(b) If u is normal then t is dominated by u iff
t factors through u, which is equivalent to that G(t)
factors through G(u) by (2.5.1.b)
as u is effective. n
Proposition 2.5.4. Suppose {ui:
Ui ® X} is a set of
open effective monos and t: T ®
X is a map.
(a) t is disjoint with each ui iff G(t)
is disjoint with the join of G(ui).
(b) t is dominated by {ui: Ui
® X} if G(t)
factors through the join of G(Ui).
Proof. (a) Assume t is disjoint with each ui. Then G(t)-1(G(Ui)) = 0 for each Ui by (2.5.3.a). Thus
(b) Suppose G(t) factors through the join of G(ui). Consider a map s: S ® T such that t°s is disjoint with each ui. Then G(t°s) is disjoint with the join of G(ui) by (a). But G(t°s) also factors through the join of G(ui) because G(t) is so. This means that G(t°s) is the initial locale. Hence S is initial by (2.5.2.a). This shows that t is dominated by {ui}. n
Denote by D(G) the class of open effective monos for a framed topology G.
Proposition 2.5.5. D(G) is a submonic divisor.
Proof. Clearly the isomorphisms are open effective. The initial
maps are open effective as a consequence of (2.5.2.a).
We prove that D(G) is closed
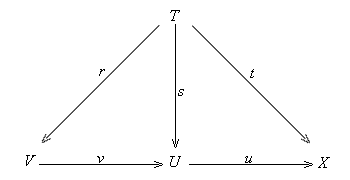
under composition. Suppose u: U ®
X and v: V ® U
are two open effective monos. Then G(u°v)
= G(u)°G(v)
as a composite of open embeddings of locales is an open embedding. If t:
T ® X is a map in A
such that G(t) factors through G(u)°G(v),
then t factors through u uniquely in a map s: T
® U because u is open
effective and G(t) factors through G(u).
It follows that s factors through v in a map r:
T ® V as v is open effective
and G(s) factors through G(v).
This shows that t factors through u°v.
Thus u°v is open
effective.
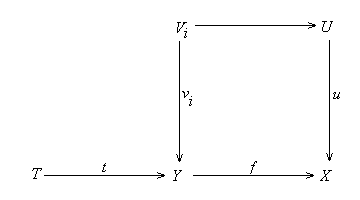 n
nThe monic divisor D(G) is called the open divisor of G.
Proposition 2.5.6. Any open effective cover is a unipotent cover.
Proof. Suppose {Ui} is an open effective cover on X. Then G(X) is the join of {G(Ui)}. Applying (2.5.4.b) we see that the identity map X ® X is dominated by {ui: Ui ® X}. Thus {ui} is a unipotent cover on X. n
Proposition 2.5.7. The collection T(G) of open effective covers is a unipotent Grothendieck topology on A.
Proof. We verify the three conditions of a Grothendieck topology
for T(G) (cf. (2.3.4)).
(a) Clearly any isomorphism is an open cover and the empty set is an
open cover only on 0 .
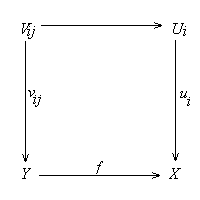
(b) Suppose {ui: Ui ®
X} is an open cover on X and f: Y ®
X is any map. Then each G(f)-1(G(Ui)
is a join of open effective sublocales {G(vij):
G(Vij) ®
G(Y)}. Since G(Y)
is the join of {G(f)-1(G(ui)},
it is the join of {G(vij)}.
Thus {vij: Vij ®
Y} is an open effective cover on Y such that for each ij,
f°vij
factors through ui.
These together with (2.5.6) show that T(G) is a unipotent Grothendieck topology on A. n
Remark 2.5.8. If A has pullbacks then one can show that the open divisor D(G) of any framed topology G is a stable divisor (see [L2]).
Suppose G is a framed topology on A.
A sieve U on an object X is called open if it is the
pullback of an open embedding v: V ®
G(X) of locales (i.e., a map s
is in U iff G(s) factors through
v); an open sieve is effective
if it is generated by an open effective mono. The set of open sieves on
X is a locale isomorphic to G(X)
naturally. Thus a framed topology can be defined intrinsically as a function
which assigns to each object a locale of sieves (cf. [Luo
1995b].