3.3. Simple Objects 

Definition 3.3.1. (a) A mono (or subobject) is called a fraction if it is coflat and normal. 
(b) A map to an object X is called generic if it is not disjoint with any non-initial analytic subobject of X. 

Proposition 3.3.2. (a) The class of fractions is closed under composition and stable under pullback. 
(b) If f: Y --> X is a fraction and U is a strong subobject of Y, then U --> f+1(U) is a fraction. 
(c) If f: Y --> X is a fraction which factors through a mono u: U --> X in a map v: Y --> U, then v is a fraction. 
(d) Any proper fraction of an object is disjoint with a non-initial strong subobject. 

Proof. (a) The classes of coflat maps and normal monos are closed under composition and stable under pullback. 
(b) Since f is coflat, we have f-1f+1(U) = U by (1.5.4). Thus U --> f+1(U) is the pullback of f along u: f+1(U) --> X, therefore is a fraction by (a). 
(c) The mono v is the pullback of f along u, thus is fractional by (a). 
(d) Suppose U is a proper fraction of an object X. Since U is normal, U is disjoint with a non-initial map t: T --> X, and we may assume t is a strong mono by (1.5.2). –– 

Definition 3.3.3. (a) A map to an object X is called local if it is not disjoint with any non-initial strong subobject of X; a non-initial object is called pseudo-simple if any non-initial map to it is local. 
(c) A map to an object X is called quasi-local if it does not factor through any proper fraction to X; a non-initial object is called quasi-simple if any non-initial map to it is quasi-local. 
(d) A map to an object X is called prelocal if it does not factor through any proper analytic mono to X; a non-initial object is called presimple if any non-initial map to it is prelocal. 

Proposition 3.3.4. (a) Any local map is quasi-local; any quasi-local map is prelocal. 
(b) The class of local (resp. generic, resp. quasi-local, resp. prelocal) maps is closed under composition. 
(c) A quasi-local fraction (resp. prelocal analytic mono) is an isomorphism. 
(d) If f: Y --> X and g: Z --> Y are two maps and gf is local (resp. generic, resp. quasi-local, resp. prelocal) then f is local (resp. generic, resp. quasi-local, resp. prelocal). 
(e) Any unipotent map is both local and generic. 
(f) Any epi is generic. 
(g) If f: Y --> X is a generic map and Y is quasi-primary then X is quasi-primary. 

Proof. (a) Any proper fraction u: U --> X is disjoint with a non-initial strong subobject V of X by (3.3.2.d). Any local map f: Y --> X is not disjoint with V, therefore f does not factor through any proper fraction U. The second assertion is trivial. 
(b) Consider two local maps f: Y --> X and g: Z --> Y. Suppose fg is disjoint with a strong mono v: V --> X. Then f-1(V) --> Y is disjoint with g:  Since g: Z --> Y is local this implies that f-1(V) is initial. Thus f is disjoint with V. Since f is local, V is initial. This shows that fg is local. The proof for generic maps is similar. 

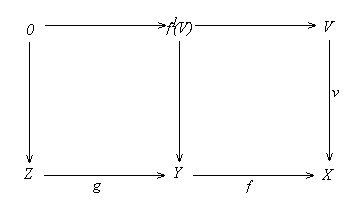
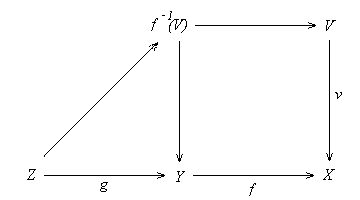
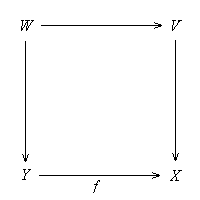
Consider two quasi-local maps f: Y --> X and g: Z --> Y. Suppose f°g factors through a fraction v: V --> X. Then g factors through f-1(V). Since g is quasi-local and f-1(V) --> Y is a fraction, we have f-1(V) = Y. Thus f factors through V, so V = X as f is quasi-local. This shows that gf is quasi-local. The proof for prelocal maps is similar. 
(c) - (e) are obvious. 
(f) If f: Y --> X is an epi then its pullback along any non-initial analytic mono V --> X is a non-initial epi W --> V, thus f is not disjoint with V --> X. Hence f is generic. 
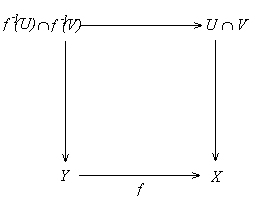
(g) Consider two non-initial analytic subobjects U and V of X. Since f is generic, the analytic subobjects f-1(U) and f-1(V) of Y are non-initial. Since Y is quasi-primary, f-1(V)  f-1(U) is non-initial. Since the induced map f-1(V)  f-1(U) --> X of f factors through U  V, it follows that U  V is non-initial. Thus X is quasi-primary. 

Recall that an epi e is called extremal provided that it does not factors through a proper mono. Every regular epi is an extremal epi. 

Definition 3.3.5. A non-initial object is called simple (resp. extremal simple, resp. unisimple) if any non-initial map to it is epic (resp. extremal epic, resp. unipotent). 

Proposition 3.3.6. An object X is simple (resp. extremal simple, resp. unisimple, resp. quasi-simple, resp. presimple) iff it has exactly two strong subobjects (resp. subobjects, resp. normal sieves, resp. fractions, resp. analytic subobjects). 

Proof. A non-initial strong subobject V of a simple object is determined by an epic strong mono, which must be an isomorphism by (1.1.2.b), thus V = X. Conversely, assume X has exactly two strong subobjects; then X is non-initial. If t: T --> X is any non-initial map then t+1(T) is a non-initial strong subobject of X, thus t+1(T) = X, so t is epic. 
A non-initial subobject V of an extremal simple object X is an extremal epic mono, so V = X. Conversely if X has exactly two subobjects, any non-initial map t: T --> X must be extremal epic. 
Any non-initial map to a unisimple object is unipotent, thus generates the maximal normal sieve. This implies that X has exactly two normal sieves. Conversely if X has exactly two normal sieves, any non-initial map to X generates the maximal normal sieve, thus it is unipotent. 
A non-initial fraction to a quasi--simple object is a quasi-local fraction, thus is an isomorphism by (3.3.4.c). Conversely, if X has exactly two fractions then any non-initial map is quasi-local, so it is quasi-simple. The proof for the case of presimple objects is similar. 

Proposition 3.3.7. (a) Any simple object is integral. 
(b) Any extremal simple object and any reduced unisimple object is simple. 

Proof. (a) Any simple object is reduced and primary (cf (3.3.6), (3.1.2.a) and (3.2.1.a)). 
(b) Clearly any extremal simple object is simple by (3.3.6). Any non-initial map f to an object X is unipotent if X is unisimple, and is epic if furthermore X is reduced. Thus any reduced unisimple object is simple. 

Proposition 3.3.8. (a) A non-initial object is pseudo-simple iff any non-initial strong subobject is unipotent. 
(b) Any simple object, extremal simple object, and unisimple object is pseudo-simple. 
(c) Any pseudo-simple object is quasi-simple. 
(d) Any quasi-simple object is presimple. 
(e) Any presimple object is primary. 

Proof. (a) By definition a non-initial object X is quasi-simple iff any non-initial map to it is not disjoint from any non-initial strong mono. This implies that any non-initial strong mono is unipotent. 
(b) Any non-initial strong mono to a simple or extremal simple object is an isomorphism. Any non-initial strong mono to a unisimple object is unipotent. By (a) these objects are pseudo-simple. 
(c) and (d) follow from (3.3.4.a) 
(e) Any non-initial analytic mono to a presimple object is an isomorphism, thus any presimple object is primary. 

Proposition 3.3.9. (a) Any reduced pseudo-simple object is simple. 
(b) Any non-initial strong subobject of a pseudo-simple object is pseudo-simple. 
(c) The radical of any pseudo-simple object is simple. 

Proof. (a) Suppose X is a reduced pseudo-simple object. By (3.3.8.a) any non-initial strong mono to X is unipotent, therefore is epic, thus is an isomorphism. It follows that X is simple by (3.3.6). 
(b) Suppose V is a non-initial strong subobject of a pseudo-simple object X . Then any non-initial strong subobject W of V is also a strong subobject of X , thus W is a unipotent subobject of X. It follows that W is also a unipotent subobject of V. Thus V is pseudo-simple by (3.3.8.a). 
(c) follows from (a) and (b). 

Proposition 3.3.10. Suppose A is locally disjunctable in which each object has a radical. The following are equivalent for an object X : 
(a) X is pseudo-simple. 
(b) X is quasi-simple. 
(c) X is presimple. 
(d) The radical of X is simple. 

Proof. (a) implies (b) and (b) implies (c) by (3.3.8). Assume X is presimple. Any proper strong subobject V of its radical rad(X) is not unipotent in X, thus it is disjoint with a non-initial analytic mono u: U --> X to X by (3.1.10). Since X is presimple, U = X by (3.3.6). Thus V is initial. This shows that rad(X) is simple. Thus (c) implies (d). Finally assume X is an object whose radical rad(X) is simple. We prove that it is pseudo-simple. Suppose V is a non-initial strong subobject of X. Its radical rad(V) is a non-initial strong subobject of rad(X), therefore we have rad(V) = rad(X) as by assumption rad(X) is simple. Since rad(X) is unipotent, V is unipotent. Thus X is pseudo-simple by (3.3.8.a). 

Proposition 3.3.11. Suppose any coflat unipotent map in A is regular epic and any map to a simple object is coflat. Then 
(a) Any coflat mono is normal. 
(b) Any simple object is extremal simple and unisimple. 

Proof. (a) Consider a coflat mono u: U --> X. To see that u is normal it suffices to prove that any pullback of u is not proper unipotent. Consider the pullback v: V --> Y of u along a map f: Y --> X. If v is unipotent then the coflat unipotent mono v is a regular epi by assumption, so is an isomorphism because any regular epic mono is isomorphic. 

(b) Consider a simple object P. We first show that P is unisimple. Consider two non-initial maps t: T --> P and s: S --> P. By assumption s and t are coflat epic. Thus the pullback of (s, t) is non-initial. This show that P is unisimple. Next we prove that P is extremal simple. Any non-initial subobject V of P is coflat unipotent, thus is a regular epi. Again since any regular epic mono is isomorphic, we have V = P as desired.  
 
Example 3.3.11.1. The category of affine schemes satisfies the conditions of (3.1.11). Thus any coflat mono of affine schemes is normal and any simple object (i.e. the spectrum of a field) is extremal simple and unisimple. 
 
[Next Section][Content][References][Notations][Home]