1.5. Beck-Chevalley Condition 

For any object X denote by R(X) the set of strong subobjects of X. Since A has finite limits, the poset R(X) has meets. Suppose u: U ® X and v: V ® X are two strong subobjects. Suppose T = U + V is the sum of U and V and t: T ® X is the map induced by u and v. Then the strong image t(T) of T in X is the join U Ú V of U and V in R(X). It follows that R(X) has joins. Thus R(X) is a lattice, with 0X: 0 ® X as zero and 1X: X ® X as one. An object Z has exactly one strong subobject (i.e. 0Z = 1Z) iff it is initial. 

If u: U ® X is a mono, we denote by f-1(u) the pullback of u along f. Then f-1: R(X) ® R(Y) is a mapping preserves meets such that f-1(0X) = 0Y and f-1(1X) = 1Y (i.e. f-1 is bounded ). Also f-1 has a left adjoint f+1: R(Y) ® R(X) sending each strong subobject v: V ® Y to the strong image of the composite f.v: V ® X . If V = Y then f+1(Y) is simply the strong image of f. 

Proposition 1.5.1. Suppose x: X1 ® X and f: Y ® X are two maps and f is coflat. Let y: Y1 ® Y be the pullback of x along f. Then f-1(x+1(X1)) = y+1(Y1). 

Proof. Let e: X1 ® x+1(X1) and m: x+1(X1) ® X be the epi-strong-mono factorization of x. Form the pullback 

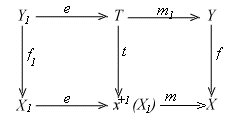
We have y = m1.e1 and T = f-1(x+1(X1)). The map m1 as the pullback of the strong mono m is a strong mono. The map t as the pullback of the coflat map f is coflat. Thus the pullback e1 of the epi e along t is also epi. Therefore (e1, m1) is the epi-strong-mono factorization of t. Thus 
y+1(Y1) = T = f-1(x+1(X1)). n

Corollary 1.5.2. If x: X1 ® X is a map which is disjoint with a coflat map f: Y ® X , then the strong image of x is disjoint with f. 

Proof. We shall use the notation and diagram in the proof of (1.5.1). Since x and f are disjoint, the pullback Y1 of x and f is 0 . The map e1: 0 = Y1 ® T is an isomorphism as it is an epic strong mono. It follows that f and m are disjoint. n 
 
Proposition 1.5.3. If f: Y ® X is a coflat map, then f-1: R(X) ® R(Y) is a morphism of bounded lattice. 

Proof. Since f-1 is bounded and preserves meets, we only need to verify that it also preserves joins. Suppose u: U ® X and v: V ® X are two strong subobjects. Let x: U + V ® X be the map induced by u and v. Then x+1(U + V) is the join of U and V . Since sums are stable, the pullback Y1 of U + V along f in the following pullback diagram is f-1(U) + f-1(V). 

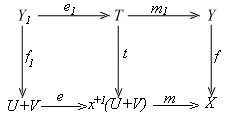
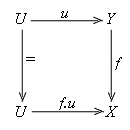
Since e1: Y1 ® T is epic, T = f-1(U) Ú f-1(V). Applying (1.5.1) we obtain T = f-1(x+1(U + V)) = f-1(U Ú V). This shows that f-1(U Ú V) = f-1(U) Ú f-1(V). n 
 
Proposition 1.5.4. If f: Y ® X is a coflat mono, then f-1f+1 is the identity R(Y) ® R(Y). 

Proof. Suppose u: U ® Y is a strong mono. Consider the mono f°u: U ® X , whose pullback along f is u . 

Applying (1.5.1) we obtain 
U = u+(U) = f-1((f°u)+1(U)) = f-1(f+1(U)). n

Proposition 1.5.4 is a special case of the following Beck-Chevalley condition for strong subobjects along coflat maps: 

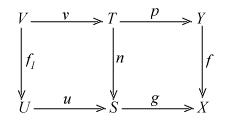
Proposition 1.5.5. Suppose f: Y ® X is a coflat map and g: S ® X is a map. Let (p: T ® Y, n: T ® S) be the pullback of (f, g). Then p+1n-1 = f-1g+1. 

Proof. Form the pullback for a strong mono u: U ® S 

We have 
V = n-1(U)
 p+1(V) = (p°v)+1(V)
g+1(U) = (g°u)+1(U).
Applying (1.5.1) to the composite x = g°u: U ® X one has 
(p°v)+1(V) = f-1((g°u)+1(U)).
Combining all of these one has 
p+1(n-1(U)) = p+1(V) = (p°v)+1(V) = f-1((g°u)+1(U)) = f-1(g+1(U)). n
 [Next Section][Content][References][Notations][Home]