Let A be a strict coherent analyitc geometires. 

Proposition 5.5.1. (a) Suppose W  X is a proper strong subobject. There is a prime V of X such that the localization X_V is not contained in W. 
(b} Let L(X) be the coproducts of all localization l_P: X_P --> X and let e: L(X) --> X be the map induced by l_P. Then e is epic. 

Proof. Since any proper strong subobject is contained in a proper regular subobject, and any proper regular subobject is an intersection of proper finitely cogenerated regular subobjects by (4.1.3), it suffices to prove the assertion for a proper finitely cogenerated regular subobject W. First we note that there is a prime V of X such that any analytic neighborhood U of V is not contained in W. Otherwise W contains an analytic cover {U_i} of X, which is not the case as the category is strict, therefore X is the colimit of {U_i  U_j}, and this only happens if X = W. Thus let V be such a prime. The localization X_V of X at V is the cofiltered limit of all the analytic neighborhoods of V . Assume X_V is contained in W. Suppose W is the equalizer of a pair (r₁, r₂): X --> T of maps with T finitely copresentable. There is an open neighborhood u: U --> X of V such that r₁v = r₂v (see the proof of (4.1.4)). Then V  U which contradicts to the choice of V. This shows that X_V is not contained in W. 
(b) e does not factors through any proper strong subobject by (a), thus is epic. 

Proposition 5.5.2. An object is reduced iff each of its localization is reduced. 

Proof. Suppose X is reduced. By (3.1.3.e) analytic subobjects of X are reduced. Any localization of X is a cofiltered limit of analytic subobjects of X, thus is reduced by (5.1.5.b). 
Conversely, assume each localization is reduced. Consider a proper strong subobject W of X. By (5.5.1) there is a localization L of X which is not contained in W, i.e. L  W is a proper strong subobject of L. As L is reduced, L  W is not unipotent. This implies that W is not unipotent as the pullback of any unipotent map is unipotent. Thus X is reduced by (3.1.2.a). 

Proposition 5.5.3. A map f: Y --> X is epic iff its pullback along any localization of X is so. 

Proof. The pullback of any epi along a localization is epic as any localization is coflat. 
Conversely assume f is not epic. Then f factors through a proper regular subobject v: V --> X in a map g: Y --> V. According to (5.5.1.a) there is a localization l: L --> X which does not factor through V. Let (u: L  V --> L, w: L  V --> V) be the pullback of (v, l). Then u: L  V --> L is a proper strong subobject of L. Let m: M --> L  V be the pullback of g along w. Then um is the pullback of f = vg. Since um factors through the proper strong subobject L  V of L, it is not epi. 

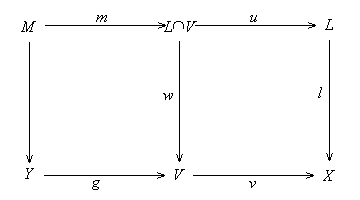Proposition 5.5.4. Suppose f: Y --> X is a mono. 
(a) If the residue maps of f are isomorphisms, then Spec(f) is injective. 
(b) If f is a local isomorphism then Spec(f) is injective. 

Proof. (a) Suppose P  Spec(Y) and Q  Spec(Y) are two primes over the same O  Spec(X). Then their  residues k(P) and k(Q) are isomorphic to the residue k(O) of O by assumption. Thus there are isomorphisms u: k(P) --> k(O) and v: k(Q) --> k(O). Let s (resp. t) be the compositions of u^-1: k(O) --> k(P) (resp. v^-1: k(O) --> k(Q)) with the inclusions k(P) --> Y (resp. k(Q) --> Y ). Then fs = ft is the inclusion k(O) --> X. Since f is a mono, we have s = t. So P = Q. This shows that Spec(f) is injective. 
(b) follows from (a) as the residue maps of a local isomorphism are isomrophisms. 

Proposition 5.5.5. Suppose f: Y --> X is a  map. 
(a) If f is unipotent then Spec(f) is surjective. 
(b) If f is coflat and Spec(f) is surjective then it is unipotent. 
(c) Assume f is coflat and X is local. Then f is unipotent iff the simple prime of X is contained in the image of Spec(f). 

Proof. (a) If Spec(f) is not surjective we can find a residue P --> X which does not factors through f, then P --> X is disjoint with f, thus f is not unipotent. 
(b) We may assume that f is non-initial. Consider a non-initial map t: T --> X. Let p: P --> X be the generic residue of a prime in the image of Spec(t). Let u: F --> P be the pullback of f along p, and let v: G --> P be the pullback of t along p. Then F and G are not initial as P is in the image of Spec(f) and Spec(t). Since u as the pullback of a coflat map is coflat, and v is epic as a non-initial map to a simple object, the fibre product W of u and v is epic over F, thus is non-initial. The following commutative diagram implies that t and f are not disjoint, thus f is unipotent. 

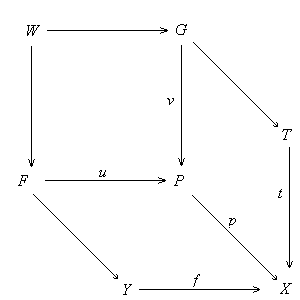Proposition 5.5.6. Any unipotent local isomorphic mono f: Y --> X is an isomorphism. 

Proof. First note that Spec(f) is bijective by (5.5.4) and (5.5.5). Let Z be the coproducts of all localization l_P: Y_P --> Y and let z: Z --> Y be the map induced by l_P, then z is an epi by (5.5.1.b). Since f is a local isomorphism and Spec(f) is bijective, Z is also naturally the coproducts of localizations of X with fz: Z --> X as the canonical map. Thus fz is epic by (5.5.1.b), which implies that f is epic. Since finitely copresentable objects form a strong generating set of A, to see that f is an isomorphism, it suffices to prove that any map t: Y --> C from Y to a finitely copresentable object C factors through f. Suppose p: Y_P --> Y is a localization of Y at a prime P. Since f is a local isomorphism, fp: Y_P --> X is the localization of X at f⁺¹(P). Thus Y_P is the cofiltered limit of a collection of analytic neighborhoods V_i of f⁺¹(P) with the maps (fp)_s: Y_P --> V_i. Since C is finitely copresentable, there exists an analytic neighborhood V_s of f⁺¹(P) and a map g_s: V_s --> C such that t_s p_s = g_s f_sp_s, where t_s: f^-1(V_s) --> C, p_s: Y_P --> f^-1(V_s) and f_s: f^-1(V_s) --> V_s are the induced maps. Since C is finitely copresentable and Y_P is the filtered limits of open analytic neighborhood of P, and f^-1(V_s) is one of such analytic neighborhood, there is a small analytic neighborhood U_P contained in f^-1(V_s) such that the restrictions of t_s and g_s f_s on U_P are the same, denoted this restriction by t_P . We have proved that for any prime P we can find a small open neighborhood U_P of P such that the restriction of t on U_P can be factored through the restriction of f on U_P. Since the analytic category is strict, these factorization can be glue together to obtain a global factorization for t by f. 

Proposition 5.5.7. A mono is a local isomorphism iff it is a fraction. 

Proof. Suppose u: U --> X is a local isomorphic mono. Any unipotent pullback of u is a unipotent local isomorphic, therefore is an isomorphism by (5.5.6). Thus u is normal. So we only need to prove that u is coflat. Since the class of local isomorphisms is closed under pullback, it suffices to prove that u is precoflat. Suppose t: T --> X is an epi and r: Z --> U, s: Z --> T is the pullback of f and t. For any localization g: G --> U the map r^-1(U) --> U is epic because it is the pullback of the epic map t along the localization ug: G --> X. This shows that if r factors through a strong mono w: W  U, then W contains all the localization of U. This is only possible if W = U by (5.5.1.a). This shows that r is epic, which means that  u is precoflat as desired. The other direction has been proved in (5.3.3).