Definition 3.2.1. (a) A non-initial
object is primary
if any non-initial analytic mono to it is epic.
(b) A non-initial object is quasi-primary
if any two non-initial analytic monos are not disjoint with each other.
(c) An integral
object is a reduced primary object.
(d) A prime
of an object is an integral strong subobject.
(e) A non-initial object is irreducible
if it is not the join of two proper strong subobjects.
Proposition 3.2.2. (a) Any quotient
of a primary object is primary.
(b) If f: Y ® X
is a map and U a primary subobject of Y, then the strong
image f+1(U) of f in X is a primary
subobject of X.
(c) Any primary object is quasi-primary.
Proof. (a) Let f: Y ® X be an epi with Y primary. Consider any non-initial analytic mono t: T ® X. Let (g: W ® Y, h: W ® T) be the pullback of (t, f). Then h is non-initial epic as it is the pullback of an epi along the non-initial coflat map t, and g as the pullback of an analytic mono is a non-initial analytic mono, so g is epic as Y is primary. It follows that f°g = t°h is epic, and so t is epic.
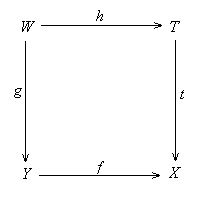
(c) Suppose U and V are two non-initial analytic subobject of a primary object X. Since U and V are coflat and epic, U Ç V is an epic analytic mono of U and V (cf. (1.6.6.b)), thus is non-initial. –––n
Corollary 3.2.3. (a) Any quotient of
an integral object is integral.
(b) If f: Y ® X
is a map and U a prime of Y, then f+1(U)
is a prime of X.
Proof. (a) follows from (3.2.2.a) and (3.1.3.a).
(b) follows from (3.2.2.b) and (3.1.3.b).
––n
Proposition 3.2.4. (a) Any non-initial
analytic subobject of a primary object is primary.
(b}Any non-initial analytic subobject of an integral object is integral.
Proof. (a) Suppose u: U ®
X is a non-initial analytic subobject of a primary object X.
Consider a non-initial analytic subobject t: T ®
U. Since u°t
is analytic and X is primary, u°t
is epic, so t is epic (as the pullback of the epi u°t
along the coflat mono u), thus U is primary as desired.
(b) follows from (a) and (3.1.3.e).
––n
Proposition 3.2.5. Suppose X = U
Ú V is the join of two strong
subobjects U and V of X.
(a) If t: T ® X
is a coflat map which is disjoint with V then it factors through
U.
(b) If U and V are disjunctable then Uc
and Vc are disjoint.
Proof. (a) By (1.5.3) we have
(b) Uc Ç Vc = (U Ú V)c = Xc is initial by (1.6.4). ––n
Proposition 3.2.6. Suppose A
is locally
disjunctable. The following are equivalent for a non-initial reduced
object X:
(a) Any non-initial coflat map to X is epic.
(b) X is primary (i.e. X is integral).
(c) X is quasi-primary.
(d) X is irreducible.
Proof. Clearly (a) implies (b), and (b) implies (c) by (3.2.2.c).
We prove that (c) implies (d). Assume X is not irreducible. Then
X = U Ú V is the join of
two proper strong subobjects U and V. Since A
is locally disjunctable, we may assume U and V are disjunctable.
Since X is reduced, Uc and Vc
are non-initial, and they are disjoint by (3.2.5).
Thus X is not quasi-primary. Hence (c) implies (d).
Next we show that (d) implies (b). Assume X is irreducible.
Consider a non-initial analytic subobject U, which is the complement
of a proper strong object V of X . We prove that U
is epic. Consider any strong subobject W of X containing
U. Since W Ú V contains
U = Vc and V, it is unipotent, thus X = W Ú
V as X is reduced. Since V is proper, by (d) we have
W = X. This shows that U is an epic subobject by (1.1.3.e).
This shows that (d) implies (b).
Finally we prove that (b) implies (a). Consider a non-initial coflat
map f: Y ® X. As A
is locally disjunctable, any proper strong subobject is contained in a
proper disjunctable strong subobject. To see that f is epic by (1.1.3.e)
it suffices to show that it does not factor through any proper disjunctable
strong subobject V of X. Since X is reduced, Vc
is a non-initial analytic mono, therefore epic by (b). Since f is
non-initial and coflat, f is not disjoint with Vc.
Since Vc is disjoint with V, this implies that
f: Y ® X does not factor
through any proper disjunctable strong subobject V, so it is epic.
This shows that (b) implies (a). ––n
Corollary 3.2.7. Suppose A
is locally disjunctable.
(a) An object is integral iff it is reduced and quasi-primary.
(b) An object is integral iff it is reduced and irreducible.
Proof. By (3.2.6). ––n
Later we shall prove in Section 5 that if A
is an analytic geometry then
a non-initial object X is quasi-primary iff its radical is integral.