|
5.2. Localizations
An epi f: Y ® X
is called essential
provided that for any map g: Z ®
Y, if f°g is
epic then g is epic.
Proposition 5.2.1. Suppose f:
Y ® X is a coflat map and X
is integral.
(a} If f is an essential epi then Y is integral.
(b} If f is a bimorphism then Y is integral.
Proof. Let p: P(X) ®
X be the generic residue of the integral object X, which
is an epi coflat fraction by (5.1.2.c).
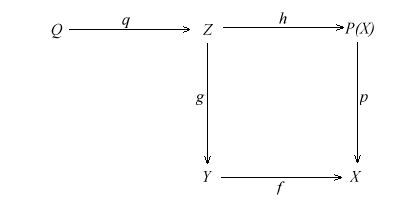
Let (g: Z ® Y, h:
Z ® P(X)) be the pullback
of (f: Y ® X, p:
P(X) ® X).
(a) Assume f is an essential epi. Since f and p
are coflat and epic, g and h are epic. Thus Z is non-initial,
which has a simple strong subobject q: Q ®
Z (4.2.2.d). Since P is simple,
h°q: Q ®
P(X) is epic. Since p is epic, p°h°q
= f°g°q
is also epic. Since f is an essential epi, g°
q: Q ® Y is epic. Then
Y, as a quotient of a simple object, is integral.
 (b) This follows from (a) as any coflat bimorphism is an essential epi.
by (1.4.4.e). n
(b) This follows from (a) as any coflat bimorphism is an essential epi.
by (1.4.4.e). n
Proposition 5.2.2. Suppose f:
Y ® X is any map. The image of
Spec(f) is {V Î Spec(X):
f+1(f-1(V)) = V}.
Proof. Suppose V = Spec(f)(W) = f+1(W)
for a prime W of Y. Then f+1f-1(V)
is a subobject of X contained in V. But W Í
f-1(V) implies that V = f+1(W)
Í f+1f-1(V).
Thus V = f+1f-1(V).
Conversely, assume V = f+1f-1(V)
holds. Consider the pullback (r: Z ®
f-1(V), s: Z ®
P(V) of the maps (u: f-1(V)
® V, p: P(V) ®
V). Since u is epic and p is coflat epic, s: Z
® p(V) is epic, thus Z
is non-initial, which has a simple subobject q: Q ®
Z. But p°s°q
= u°r°q
and the left side is epic, thus the right side u°r°q
is epic. Let W = (r°q)+1(Q).
Then u+1(W) = V. But u is the restriction
of f on f-1(V). This shows that f+1(W)
= V, i.e. V is lying in the image of Spec(f).
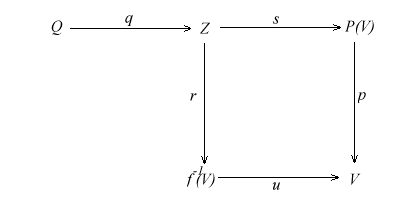 n n
Proposition 5.2.3. Suppose f:
Y ® X is a coflat map.
(a} The image of f is {V Î
Spec(X): f-1(V) is non-initial}.
(b} If V is in the image of Spec(f) and W
is a integral strong subobject containing V, then W is in
the image (i.e. the image of Spec(f) is closed under generalizations).
Proof. (a) If V is in the image then by (5.2.2)
f+1f-1(V) = V, so f-1(V)
is non-initial.
Conversely, assume f-1(V) is non-initial.
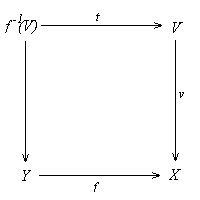
The induced map t: f-1(V) ®
V is the pullback of f along V ®
X, thus is also coflat. Since V is integral and f-1(V)
is non-initial, t is epic by (3.2.6.a).
Thus f+1f-1(V) = V, which implies
that V is in the image of Spec(f) by (5.2.2).
 (b) If V Í W are two primes
of X and V is in the image of Spec(f), then
by (a) f-1(V) is non-initial. This implies that
f-1(W) is non-initial, so W is in the image
of Spec(f) by (a). n
(b) If V Í W are two primes
of X and V is in the image of Spec(f), then
by (a) f-1(V) is non-initial. This implies that
f-1(W) is non-initial, so W is in the image
of Spec(f) by (a). n
Proposition 5.2.4. Suppose Y
is a local object with the simple prime M and f: Y ®
X is a coflat mono. Then Spec(f) induces a homeomorphism
between Spec(Y) and the subspaces of Spec(X)
consisting of primes which contains M.
Proof. Since f is a coflat mono, Spec(f)
is a topological embedding by (3.6.9.a).
Since any prime V of Y contains M, we have f+1(V)
Ê f+1(M) Ê
M. Conversely, if W is a prime of X which contains M,
then it contains f+1(M). Thus by (5.2.3.b)
it is in the image of Spec(f). n
Proposition 5.2.5. Suppose f:
Y ® X is a coflat local map of
local objects. Then Spec(f): Spec(Y) ®
Spec(X) is surjective.
Proof. By (3.4.7) the simple prime
P of X is in the image of f. Since any prime of X
contains P, by (5.2.3.b) it is in the
image of f. n
Suppose V is an integral subobject of an object X. Denote
by XV the intersection of all the analytic subobjects
of X which is not disjoint with V.
Proposition 5.2.6. Assume V is
an integral subobject of X with the generic residue P(V).
(a) XV is the intersection of all the analytic subobjects
of X containing P(V).
(b) XV is a local object whose simple prime
contains P(V).
(c) XV is the intersection of all the fractions of
X containing P(V).
(d) If V is a prime then P(V) = XV
Ç V.
Proof. (a) Since V is integral and the simple object
P(V) is the intersection of non-initial fractions of V,
an analytic subobject of X is not disjoint with V iff it
contains P(V).
(b) XV contains P(V) by (a), thus is
non-initial. We prove that any non-initial strong subobject S of
XV contains P(V), which would implies that
the intersection P'(V) of all the non-initial strong subobjects
of XV is non-initial, and therefore XV
is local whose simple prime P'(V) contains P(V).
If this is not the case, then the simple object P(V) is disjoint
with S. Since XV is a coflat subobject of X,
S is induced by a strong subobject S' such that S
= S' Ç XV. Then
P(V) is disjoint with S'. Since A
is locally disjunctable, we can find a disjunctable strong subobject T
of X such that S' Í T
and P(V) is not contained in T. Then the simple object
P(V) is disjoint with the strong subobject T, so P(V)
Í Tc, thus Tc
is not disjoint with V, so XV as the intersection
of such analytic subobjects is contained in Tc, which
is absurd as S is in XV but not in Tc
as S Í S' Í
T. This shows that any non-initial strong subobject S of XV
contains P(V), so XV is local.
(c) As P(V) ® XV
is local (thus quasi-local by (3.3.4.a)
and XV ® X is a
faction, this pair of maps is the quasi-local-fraction factorization of
the inclusion P(V) ®
X. By (4.2.9) XV
is the intersection of fractions of X containing P(V).
(d) Clearly P(V) is contained in XV
Ç V, thus XV
Ç V is non-initial, which is a
fraction of V as XV is a fraction
of X. It suffices to prove that XV Ç
V is simple. Consider a proper strong subobject S of XV
Ç V. Since XV
Ç V is a coflat subobject of V,
S is induced by a proper strong subobject S' of V,
i.e. S = (XV Ç
V) Ç S'. Since V
is a proper strong subobject of X, S' is also a proper strong
subobject of X. Since A is locally disjunctable,
we can find a disjunctable strong subobject T of X containing
S' but not V. Then T Ç
V is a proper subobject of V, and Tc Ç
V = (T Ç V)c.
Since V is reduced and T Ç
V is proper, (T Ç V)cis
a non-initial analytic subobject of V. Since by definition XV
Í Tc Ç
V = (T Ç V)c,
XV is disjoint with T Ç
V. As S Í S' Í
T Ç V, we see that XV
is disjoint with S. Since XV is non-initial
and by construction S Í XV,
this means that S is initial. We have proved that any proper
strong subobject S of XV Ç
V is initial. Thus XV Ç
V is simple. n
Proposition 5.2.7. If P is a
simple subobject of X then XP is a local object,
and XP is the intersection of all the analytic
subobjects (or fractions) of X which contains P.
Proof. The assertion follows from (5.2.6).
n
Definition 5.2.8. (a) A fraction Y
® X with a local
domain Y is called a localization.
(b) Suppose V is an integral subobject of an object X.
With the notations of (5.2.6), the localization lV:
XV ® X is called
the localization of X at
V.
Remark 5.2.9. Suppose Y
is a small strong cogenerating set formed by finitely copresentable
objects. If W is a Y-principal regular subobject
of an object X, we say that Wc is a Y-principal
analytic subobject of X. Similar to (5.2.6)
and (5.2.7) one can show that for any integral subobject
V of X, the localization XV of
X at V is the intersection of Y-principal
analytic subobjects of X which is not disjoint with V (the
key step is (5.2.6.c) to prove that the intersection
is a local object).
Proposition 5.2.10. Suppose f:
Y ® X is a localization and
P is the simple prime of the local object Y and V =
f+1(P). Then Y is the localization of X
at the prime V.
Proof. Since f is coflat, P = f-1f+1(P)
= Y Ç f+1(P)
implies that P is a epic simple fraction, thus P is the generic
residue of the prime V = f+1(P). Since
the inclusion P ® Y is local
and f: Y ® X is a fraction,
this pair of maps is the quasi-local-fraction factorization of P
® X. But the inclusion P ®
XV is also local and the inclusion XV
® X is a fraction, we obtain another
pair of maps which is also a quasi-local-fraction factorization of the
inclusion P ® X. By the uniqueness
of such a factorization we see that Y = XV as
subobjects of X. n
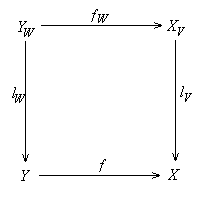
Proposition 5.2.11. Let f: Y
® X be a map. Suppose W
Î Spec(Y) and V =
f+1(W). Then there is a unique local map fW:
YW ® XV
of local objects such that the following diagram commutes:
 Proof. Since XV is the intersection of analytic
subobjects of X which is not disjoint with V, f-1(XV)
contains YW, which is the intersection of analytic subobjects
of Y that is not disjoint with W. Thus the composition W
® X of the inclusion W ®
Y and f factors through the inclusion XV
® X in a unique map fW:
YW ® XV.
Clearly f sends YW ®
W = P(W) into XV ®
V = P(V), where P(W) and P(V)
are the generic residues of W and V respectively. Thus fW
is local by (3.4.7.b).
Proof. Since XV is the intersection of analytic
subobjects of X which is not disjoint with V, f-1(XV)
contains YW, which is the intersection of analytic subobjects
of Y that is not disjoint with W. Thus the composition W
® X of the inclusion W ®
Y and f factors through the inclusion XV
® X in a unique map fW:
YW ® XV.
Clearly f sends YW ®
W = P(W) into XV ®
V = P(V), where P(W) and P(V)
are the generic residues of W and V respectively. Thus fW
is local by (3.4.7.b).
With the notation of (5.2.11) we say that XV is the local
image of the localization YW. of Y (under
f).
Definition 5.2.12. Let f: Y
® X be a map. We say that the going-up
theorem holds for f if the following condition
is satisfied:
For any V, V' Î Spec(X)
such that V Í V', and for
any W Î Spec(Y) with
f+1(W) = V, there exists W' Î
Spec(Y) with f+1(W') = V'
such that W Í W'.
Now we can prove a generalization of the dual version of the going-down
theorem for a flat homomorphism of commutative rings (cf. [Matsumura
1980, p.33, Theorem 4]):
Proposition 5.2.13. (Going Up Theorem)
The going-up theorem holds for any coflat map f: Y ®
X.
Proof. Suppose V, V' Î
Spec(X) such that V Í
V', and W Î Spec(B)
with f+1(W) = V. Consider the localization
lW: YW ®
Y, which is coflat. Then f°lW:
YW ® X is coflat.
By (5.2.3.b) V' is in the image of f°lW.
Thus there is a prime Q of YW such that f°lW+1(Q)
= V. Let W' = lW+1(Q).
Then W' contains W and f(W') = W as
desired (alternatively the theorem follows from the fact that the induced
local map YW ® XV
is local, thus the mapping Spec(YW) ®
Spec(XV) is surjective, and the fact that the
mappings Spec(YW) ®
Spec(Y) and Spec(XV) ®
X are embeddings.). n
[Next Section][Content][References][Notations][Home]
|

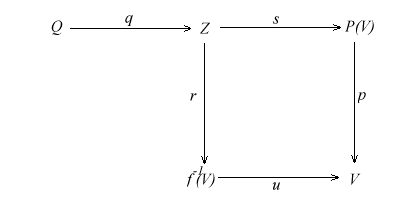 n
n 
